2014年高考理科数学真题及答案(广东卷)文字版

　　一、选择题

　　2014年全国高考将于6月7日-9日举行。

　　2014年普通高等学校招生全国统一考试(广东卷)

　　理科数学

　　一、选择题：本大题共8小题，每小题5分，满分40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

  1

　　6、已知某地区中小学生人数和近视情况分别如图1和图2所示，为了解该地区中小学生的近视形成原因，用分层抽样的方法抽取2%的学生进行调查，则样本容量和抽取的高中生近视人数分别为

（第六题图片）

　　A、200,20 B、100,20 C、200,10 D、100,10

　　7、若空间中四条两两不同的直线1，2，3，4 ，满足l垂直与2，2垂直于3，3垂直于4，则下列结论一定正确的是

　　A.1垂直于4 B.1平行于4 C. 1、4既不垂直也不平行 D. 1、4的位置关系不确定

　　8.设集合 ，那么集合A中满足条件“ ”的元素个数为

　　A.60 B90

　　二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分.

　　(一)必做题(9～13题)

　　9.不等式 的解集为 。

　　10.曲线 在点 处的切线方程为 。

　　11.从0,1,2,3,4,5,6,7,8，9中任取七个不同的数，则这七个数的中位数是6的概率为 。

　　12.在 中，角 所对应的边分别为 ，已知 ，

　　则 。

　　13.若等比数列 的各项均为正数，且 ，

　　则 。

　　(二)选做题(14～15题，考生从中选做一题)

　　14、(坐标与参数方程选做题)在极坐标系中，曲线C1和C2的方程分别为 和 =1，以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，则曲线C1和C2的交点的直角坐标为__

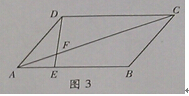
　   15、(几何证明选讲选做题)如图3，在平行四边形ABCD中，点E在AB上且EB=2AE，AC与DE交于点F，则 =___

　　三、解答题：本大题共6小题，满分80分.解答须写出文字说明、证明过程和演算步骤.

　　16、(12分)已知函数 ，且 ，

　　(1)求 的值;

　　(2)若 ， ，求 。

　　17、(13分)随机观测生产某种零件的某工厂25名工人的日加工零件数(单位：件)，获得数据如下：

　　根据上述数据得到样本的频率分布表如下：

　　(1)确定样本频率分布表中 和 的值;

　　(2)根据上述频率分布表，画出样本频率分布直方图;

　　(3)根据样本频率分布直方图，求在该厂任取4人，至少有1人的日加工零件数落在区间(30,50]的概率。

　　18、(13分)如图4，四边形ABCD为正方形，PD⊥平面ABCD，∠DPC=30，AF⊥式PC于点F，FE∥CD，交PD于点E。

　　(1)证明：CF⊥平面ADF;

　　(2)求二面角D-AF-E的余弦值。

　　19. (14分)设数列 的前 和为 ,满足 ，且 。

　　(1)求 的值;

　　(2)求数列 的通项公式;

　　20. (14分)已知椭圆 的一个焦点为 ，离心率为 ，

　　(1)求椭圆C的标准方程;

　　(2)若动点 为椭圆外一点，且点P到椭圆C的两条切线相互垂直，求点P的轨迹方程。

　　21.(本题14分)设函数 ，其中 ，

　　(1)求函数 的定义域D;(用区间表示)

　　(2)讨论 在区间D上的单调性;

　　(3)若 ，求D上满足条件 的 的集合。