2021年人教版五年级上册第六单元多边形的面积试题解析

第六单元 多边形的面积

【例1】如图面积的关系正确的是(　　)。

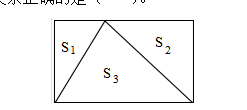
A.S1+S2=S3 B.S1=S2 C.S2=S3+S1 D.不能判断

解析：本题考查的知识点是长方形中最大的三角形的面积与长方形面积的关系。

解答时明确长方形内最大的三角形与长方形等底等高，面积等于这个长方形的面积的一半是关键。

解答：A

【例2】下图中，已知AB=BC=CD=EF=FG=GH=1dm。

(1)平行四边形AEGC的面积和平行四边形( )的面积相等，是( )。

(2)三角形AEC和三角形( )的面积相等，是( )。

(3)梯形CDHE的面积是( )，和平行四边形( )的面积相等。

解析：本题考查的知识点是利用等积变形思想解答多边形相互之间的面积关系问题。解答时，先看清要计算的的图形的形状、底和高，和哪些图形是等积变形关系。

(1)平行四边形AEGC的面积和平行四边形BFHD的面积是相等的，它们是等底等高的形状相同的两个平行四边形，底都是2分米，高是2分米，所以面积是2×2=4(平方分米)。

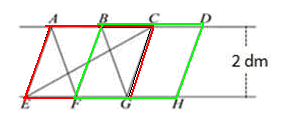
(2)三角形AEC的底是2分米，高是2分米，图中还有三角形GEC的底也是2分米，高是2分米，所以这两个三角形的面积是相等。

(3)梯形CDHE的上底是1分米、下底是3分米，高是2分米，所以面积是(1+3)×2÷2=4(平方分米)，和平行四边形AEGC或BFHD的面积相等。

解答：(1)BFHD 4dm (2)GEC 2dm (3)4 dm AEGC或BFHD

【例3】如图，4个完全相同的正方形拼成一个长方形，对图中阴影部分三角形面积的大小关系表述正确的是( )。

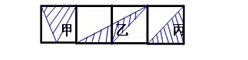
A.甲>乙>丙 B.乙>甲>丙 C.丙>甲>乙 D.甲=乙=丙

解析：本题考查的的知识点是利用等积变形思想来判断三角形的面积关系。解答时，根据三角形的面积=底×高÷2来进行判断。图中甲、乙、丙3个三角形等底等高，所以面积都相等。

如需下载完整版可以扫描下方二维码即可免费获取2021年人教版五年级上册第六单元多边形的面积试题解析电子版↓↓↓