2021年西师大版五年级上册第四单元小数混合运算试题解析

第四单元 小数混合运算

【例1】甲乙二人分别从相距3.6千米的A、B两地相向而行，甲每分钟行0.05千米，乙每分钟0.07千米，甲乙二人经过多长时间会相遇?

要点提示：

总路程÷相对速度=相遇时间。

思路分析：根据题意可知，甲行的路程加上乙行的路程就是AB两地间的距离。甲乙二人每同时行走1分钟，他们之间的距离就减少(0.05+0.07)千米，要想知道甲乙二人经过多少时间相遇，就要看AB间的距离中有多少个(0.05+0.07)千米，有几个就说明经过了几分钟才相遇。

解答： 3.6÷(0.05+0.07)

=3.6÷0.12

=30(分钟)

答：甲乙二人经过30分钟会相遇。

【例2】用简便算法计算：7.2×0.25+0.8×0.75。

要点提示：

有些表面上不符合运算的算式，可以通过等价变形转化成符合运算定律的形式，再简便运算。

思路分析：通过观察，发现7.2和0.8、0.25与0.75都有很明显的倍比关系，根据因数与积之间的关系，可以将7.2×0.25变成2.4×3×0.25=2.4×0.75，0.8×0.75变成0.8×3×0.25=2.4×0.25，然后根据乘法分配律进行计算;也可以将0.8×0.75变成0.8×3×0.25=2.4×0.25，7.2×0.25不变，然后根据乘法分配律进行计算。

解答：方法一 方法二

7.2×0.25+0.8×0.75 7.2×0.25+0.8×0.75

=2.4×0.75+2.4×0.25 =7.2×0.25+2.4×0.25

=2.4×(0.75+0.25) =0.25×(7.2+2.4)

=2.4×1 =0.25×9.6

=2.4 =2.4

【例3】有一项修水渠的工程,工程总长是18.5千米。第一期工程计划修7.5千米,18天能完成,由于采用了先进设备,结果提前3天完成。照这样的速度,剩下的工程多少天能完成?

思路分析：从问题出发,去寻求解决问题所必需的两个条件,即实际每天的工作量和剩余的工作量。这两个条件题目中都没有直接给出,需要把这两个所必需的未知条件作为问题,再去寻找解决它们所必需的条件。

分析如下图:

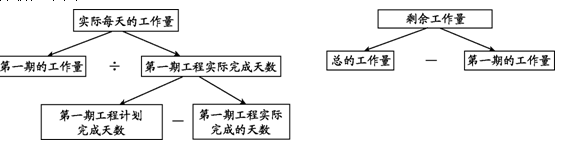
要点提示：

由问题出发去寻找解决问题的条件是关键。

解答： (18.5-7.5)÷[7.5÷(18-3)]

=11÷[7.5÷15]

=11÷0.5

=22(天)

答:剩下的工程22天能完成。

如需下载完整版可以扫描下方二维码即可免费获取2021年西师大版五年级上册第四单元小数混合运算试题解析电子版↓↓↓