例1:一座大桥长2500米,一列火车通过大桥时每分钟行980千米,从车头开上桥到车尾离开桥共需3分钟,这列火车长多少米?
解析:此题考查了混合运算,根据题意,“从车头开上桥到车尾离开桥共需3分钟。”则火车等于跑了桥的全长加上车的长度,用火车3分钟行驶的距离减去桥长2500米就是车身的长度。
答案:980×3-2500
=2940-2500
=440(米)
答:这列火车长440米。
例2:甲每小时行4.5千米,乙每小时行3.5千米,如果两人同时同地向同一方向出发,甲行进58千米后到达目的地后马上按原路返回,在途中与乙相遇,从出发到相遇经过几小时?

解析:此题考查了行程问题及混合运算。根据题意画图,
从图中可知甲在途中与乙相遇时,甲乙一共行的路程是58千米的两倍;然后根据相遇时间=总路程÷速度和,即可得到相遇时间,即58×2÷(4.5+3.5)
答案:58×2÷(4.5+3.5)
=58×2÷8
=116÷8
=14.5(小时)
答:从出发到相遇经过14.5小时。
例3:甲、乙两人分别从A、B两地同时出发,相向而行,甲每小时行48千米,乙每小时行42千米,两人在离中点18千米处相遇,求A、B两地间的距离?
解析:此题考查了行程问题,解题关键找出相遇时甲车比乙车多行多少千米。根据题意可知,两车在距重点18千米处相遇,相遇时甲车行驶的路程超过中点18千米,乙车还差18千米到达中点,也就是说甲车比乙车多行驶18×2=36千米,由于甲车每小时比乙车快48-42=6(千米),由此可以求出相遇时间,再根据速度和×相遇时间=路程,即可求出。
答案:(18×2)÷(48-42)×(48+42)
=36÷6×90
=6×90
=540(千米)
答:两地间的距离是540千米。
例4:学校食堂的张师傅去超市买带鱼,原来买15千克的钱按优惠价可以多买5千克,打折后的带鱼售价是16.8元,优惠前带鱼的单价是多少?
解析:此题考查了总价=单价×数量这个数量关系式的灵活运用。根据题意,首先根据总价=单价×数量,用打折后的价格乘以(15+5)千克,求出原来买15千克带鱼的钱是多少;然后用原来买15千克带鱼的钱除以15,即可求出优惠前带鱼的单价。
答案:16.8×(15+5)÷15
=16.8×20÷15
=336÷15
=22.4(元)
答:原来每千克22.4元。
例5:每副羽毛球拍的价钱是羽毛球价钱的14倍,现在小华买2副羽毛球拍和12个羽毛球,共210元,一副羽毛球拍和一个羽毛球各是多少钱?
解析:此题考查了等量代换。根据题意“每副羽毛球拍的价钱是羽毛球价钱的14倍”那么2副羽毛球拍就相当于14×2=28个羽毛球的价钱,210元就相当于28+12=40个,羽毛球的价钱,进而求出一个羽毛球的价钱和一副羽毛球拍的价钱。
答案:
羽毛球: 210÷(14×2+12)
=210÷40
=5.25(元)
羽毛球拍:5.25×14=73.5(元)
答:一个羽毛球的价钱是5.25元,一副羽毛球拍的价钱是73.5元。
如需下载完整版可以扫描下方二维码即可免费获取2021年冀教版五年级上册第五单元四则混合运算试题解析电子版↓↓↓
 2020春季53天天练五年级下数学人教版含答案电子版PDF免费下载
2020春季53天天练五年级下数学人教版含答案电子版PDF免费下载 五年级上册数学电子版课本(人教版)百度网盘免费下载
五年级上册数学电子版课本(人教版)百度网盘免费下载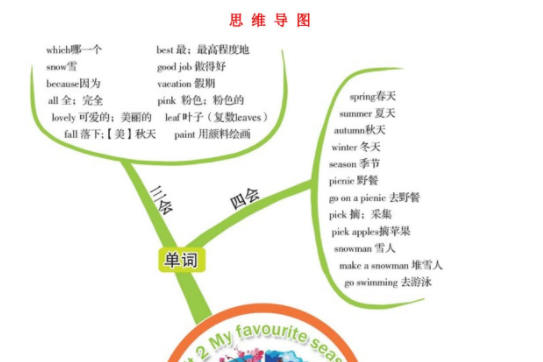 人教PEP版五年级英语下册第二单元思维导图
人教PEP版五年级英语下册第二单元思维导图 小学五年级数学上册解方程应用题100道
小学五年级数学上册解方程应用题100道 人教版五年级下册数学全册课课练电子版免费下载
人教版五年级下册数学全册课课练电子版免费下载 北师大版五年级下册数学电子课本免费下载(PDF版)
北师大版五年级下册数学电子课本免费下载(PDF版)
还没有人评论哦,赶紧抢一个沙发吧!