2021年北师大版四年级数学上册总复习试题解析

【例1】有一个五位数，最低位数字是8，最高位数字是3，个位上的数字是十位上数字的2倍，前三位数字的和与后三位数字的和都是19，这个五位数是多少?

解析：因为这是一个五位数，最低位数字是8，最高位数字是3，因此能确定万位上的数字是3，个位上的数字是8;又因为个位上数字是十位上数字的2倍，便能求出十位上的数字是8÷2=4;因为前三位数字的和与后三位数字的和都是19，所以19-8-4=7便是百位上的数字，19-3-7=9便是千位上的数字。因此这个五位数是39748。

解答：这个五位数是39748。

【例2】( )里可以填几?

49( )853≈50万 49( )853≈49万

解析：( 里的数是万位右面尾数部分的最高位上的数，用四舍

五入法把49( )853精确到万位，主要看( )里的数是“舍”还是

“入”。49( )853≈50万，说明( )里的数应该满5，才能向前一位

(万位)进1，再把尾数部分全舍去，所以( )内可以填5、6、7、8、9;

49( )853≈49万，说明( )里的数不满5，不能向前一位(万位)进

1，直接把尾数部分全舍去，所以 ( ) 内可以填0、1、2、3、4。

要点提示：

关键是看要填的数是“舍”，还是“入”。

解答： 49( )853≈50万

内可以填5、6、7、8、9。

49( )853-≈49万

内可以填0、1、2、3、4。

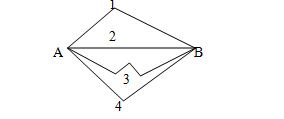
【例3】 量一量，A、B两点间的连线中，哪条最短?

要点提示：

在两点间的所有连线中，线段的长度最短。

解析： 图中A、B两点间的连线有4条，第1条和第3、4

条都是折线，第2条是直的，是线段。量一量4条连线的长

度，发现第2条连线(即线段AB)最短。

解答： 线段AB最短。

【例4】 右图中，∠1=∠2=∠3，且所有锐角的和等于1800，求∠AOB是多少度。

解析：解答此题的关键是找出此图中共有几个锐角。观察图形可知，除了∠1、∠2、∠3外，还有∠1+∠2，∠2+∠3及∠AOB这三个锐角。因此有∠1+∠2+∠3+(∠1+∠2)+(∠2+∠3)+∠AOB=1800，根据已知条件，∠l=∠2=∠3，可以求出∠AOB的度数。

解答：∠1+∠2+∠3+(∠1+∠2)十(∠2+∠3)+∠AOB=1800

因为∠1=∠2=∠3，∠AOB=∠1+∠2+∠3，

要点提示：

用计算器计算的输入顺序同笔算的顺序相似，只要按从左别右的顺序将数字和符号输入即可。

所以∠1×10=1800，∠l=1800÷10=180，∠AOB=180×3=540，

即∠AOB是540。

【例5】用计算器计算(78十56)×(63—24)。

解析：先按下 ON/C 键，打开计算器，再输入

( 7 8 + 5 6 ) × ( 6 3 - 2 4 ) ，最后输入 = ，屏幕上出现的 5226就是计算的结果。

解答： (78+56)×(63-24)=5226

如需下载完整版可以扫描下方二维码即可免费获取2021年北师大版四年级数学上册总复习试题解析电子版↓↓↓