植树问题的定义和公式

定义：按相等的距离植树，在距离、棵距、棵数这三个量之间，已知其中两个量，求第三个量。

植树问题的分类：

1.直线型植树问题(不封闭)：

①两端都植树

棵数比段数多1。

线形植树棵数=段数+1=距离÷棵距+1

距离=棵距×(棵数-1)

棵距=全长÷(棵数-1)

例题：

如图，道路的两端都植树，树有5棵(段数为4段)，棵距为2米，总长为8米。

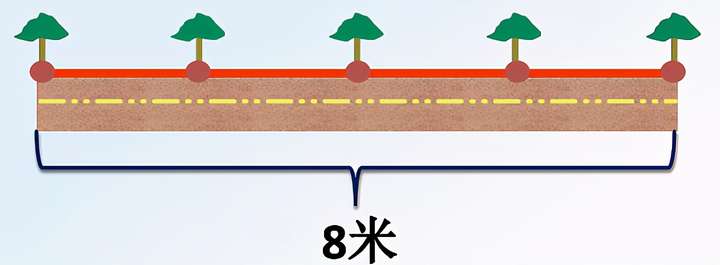
求棵数：4+1=5(颗)或8÷2+1=5(颗)

求全长：2×(5-1)=8(米)

求棵距：8÷(5-1)=2(米)

②一端植树

棵数与段数相等。

棵数=全长÷棵距

全长=棵距×棵数

棵距=全长÷棵数

例题：

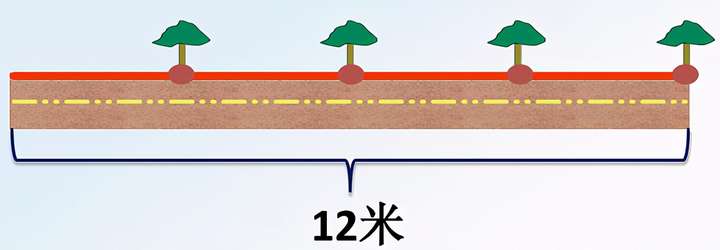
如图，一端不植树，树有4棵(段数为4段)，棵距为3米，总长为12米。

求棵数：12÷3=4(棵)

求全长：3×4=12(米)

求棵距：12÷4=3(米)

③两端都不植树

棵数比段数少1棵。

棵数=段数-1=全长÷棵距-1

全长=棵距×(棵数+1)

棵距=全长÷(棵数+1)

例题：

沿着小路的一边栽树，两端都不栽，说说你栽了几棵树，有几段间距?

2.封闭性植树问题

环形植树棵数=距离÷棵距

方形植树棵数=距离÷棵距-4

三角形植树棵数=距离÷棵距-3

3.特殊类型的植树问题

面积植树棵数=面积÷(棵距×行距)

例题：

一个圆形池塘周长为400米，在岸边每隔4米栽一棵柳树，一共能栽多少棵柳树?

解：

400÷4=100(棵)

答：一共能栽100棵柳树。

像爬楼梯的层数问题、锯木头的段数问题、敲钟遇到的时间、排队问题都与植树问题类似。

爬楼梯的层数问题，主要是要明白几层楼和几层楼之间是不一致的，楼数要比楼梯层数+1。

例题：

蓉蓉住的这栋楼共7层，每层楼梯20节，她家住在5楼，你知道蓉蓉走多少节楼梯才能到自己住的那层吗?

解：

5-1=4(层)

20×4=80(级)

答：蓉蓉走80级楼梯才能到自己住的那一层。

锯木头的段数问题，主要是要明白锯成木头的段数比锯木头的次数+1。

例题：

把一根木头锯断，要2分钟，把一根木头锯成4段，需要几分钟?

解：

2×(4-1)=6(分)

答：锯成4段，需要6分钟。

敲钟遇到的时间问题，先要考虑敲的次数比敲的间隔数+1。

时钟4点钟敲4下，用12秒敲完。那么6点钟敲6下，几秒钟敲完?

解：

时钟敲4下，经历了3个时间间隔，每隔时间间隔是：

12÷(4-1)=4(秒)

敲6下需要：4×(6-1)=20秒

答：6点钟敲6下，需要20秒敲完。

排队问题，主要是考虑排队的人数比每两个人之间的间隔+1。

例题：

同学们上体育课，有10个男生排成一排，相邻的两个男生间隔1米，请问这排男生排列的长度有多少米?

解：

1×(10-1)=9(米)

答：

这排男生排列的长度有9米。

总而言之，解答这类应用题，同学们应该先找到间隔数之间的关系，结合题目所给的已知条件和问题，就能找到解决问题的方法了。